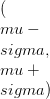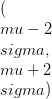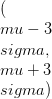ההבדל בין התפלגות בינומית ונמוכה

בינומית לעומת התפלגות נורמלית

התפלגות ההסתברות של משתנים אקראיים ממלאת תפקיד חשוב בתחום הסטטיסטיקה. מתוך חלוקות ההסתברות הללו, התפלגות בינומית והתפלגות נורמלית הם שניים מהמקרים הנפוצים ביותר בחיים האמיתיים.

מהי התפלגות בינומית?

ההפצה הבינומית היא התפלגות ההסתברות המתאימה למשתנה האקראי X, שהוא מספר ההצלחות של רצף סופי של ניסויים של כן / לא עצמאיים, שלכל אחד מהם יש הסתברות של הצלחה p. מתוך ההגדרה של X, מתברר כי הוא משתנה אקראי בדידים; לכן, ההפצה הבינומית היא גם בדידה.

- <->

ההפצה מסומנת כ- X ~ B (n, p) שבו n הוא מספר הניסויים ו- p הוא ההסתברות להצלחה. לפי תיאוריית ההסתברות, אנו יכולים להסיק כי B (n, p) עוקב אחר פונקצית המסת ההסתברות

. משוואה זו ניתן להסיק עוד כי הערך הצפוי של X, E (X) = np והשונות של X, V (X) = np (1- p).

לדוגמה, לשקול ניסוי אקראי של הטלת מטבע 3 פעמים. הגדרת הצלחה כמו קבלת H, כישלון כמו קבלת T ומשתנה אקראי

X כמספר ההצלחות בניסוי. לאחר מכן X ~ B (3, 0. 5) ותפקוד המסת ההסתברות של X שניתן על ידי. לכן, ההסתברות לקבל 2 H לפחות היא P (

X ≥ 2) = P <(X = 2 או X = 3) = P < X + 2 (+ X = 3) = 3 C 2 ^{(0 2} ) (0) ₁ ) + ³ C ³ (0) 5 ³ ) (0) 5 _{0) = 0. 375 + 0. 125 = 0. 5} -> -> ^{מהי התפלגות נורמלית?} הפצה רגילה היא התפלגות ההסתברות המתמשכת המוגדרת על ידי פונקצית צפיפות ההסתברות, ^{. הפרמטרים} מציינים את הממוצע ואת סטיית התקן של אוכלוסיית העניין. כאשר

ההפצה נקראת חלוקה רגילה רגילה.

התפלגות זו נקראת נורמלית מאחר שרוב התופעות הטבעיות עוקבות אחר ההתפלגות הנורמלית. שכן, למשל, מנת המשכל של האוכלוסייה האנושית מופצת בדרך כלל. כפי שניתן לראות מן התרשים הוא אינו יחיד, סימטרי על הממוצע ועל פעמון בצורת. ממוצע, מצב, חציון הם חופפים. השטח מתחת לעיקול מתאים לחלק של האוכלוסייה, לספק מצב נתון.

חלקים של האוכלוסייה במרווח

,

,

הם בערך 68.2%, 95. 6% ו 99. 8% בהתאמה.

-> ->

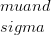
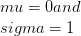
מה ההבדל בין התפלגות בינומית לבין רגילה?

הפצה בינומית היא התפלגות הסתברות דיסקרטית ואילו ההתפלגות הנורמלית היא מתמשכת.

פונקציית המסת ההסתברות של ההתפלגות הבינומית היא

, בעוד שפונקציית צפיפות ההסתברות של ההתפלגות הנורמלית היא

ההתפלגות הבינומית קרובה להתפלגות נורמלית בתנאים מסוימים, אך לא להפך.