ההבדל בין אינטגרלים מוגדרים ואינסופיים ההבדל בין

חשבון הוא ענף חשוב במתמטיקה, והבחנה משחקת תפקיד קריטי בחישוב. התהליך ההופכי של ההבחנה נקרא אינטגרציה, וההופך נקרא אינטגרל, או פשוט לשים, ההופך של בידול נותן אינטגרל. בהתבסס על התוצאות הם מייצרים את האינטגרלים נחלקים לשני סוגים דהינו., אינטגרלים מוגדרים ובלתי מוגדרים.

מוגדר אינטגרל

-> ->

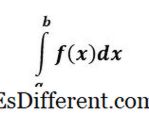
האינטגרל המובהק של f (x) הוא מספר ומייצג את האזור מתחת לעיקול f (x) מ x = a עד x = b .

אינטגרל מסוים יש גבולות עליון ותחתון על אינטגרלים, וזה נקרא מוגדר, כי בסוף הבעיה, יש לנו מספר - זה תשובה ברורה.

-> ->

בלתי מוגדר אינטגרל

אינטגרל בלתי מוגדר של f (x) הוא פונקציה עונה על השאלה, "מה פונקציה כאשר מובחנת נותן f (x) ? "עם אינטגרל בלתי מוגבל אין גבולות עליון ותחתון על אינטגרל כאן, ומה נקבל היא תשובה כי עדיין יש

x זה יהיה גם יהיה קבוע (מסומן בדרך כלל על ידי C ).

אינטגרל בלתי מוגדר בדרך כלל נותן פתרון כללי למשוואה הדיפרנציאלית.

אינטגרל בלתי מוגדר הוא צורה כללית יותר של אינטגרציה, וניתן לפרש אותו כאנטי-נגזרת של הפונקציה הנחשבת.

נניח שהבחנה של פונקציה

F מובילה לפונקציה אחרת f , והאינטגרציה של F נותנת את האינטגרל. באופן סמלי, זה כתוב כ- F (x) = ∫ƒ (x) dx

או

F = ∫ƒ dx

כאשר שניהם

F ו- ƒ < הם פונקציות של x , ו- F ניתנות לשינוי. בצורתו הנ"ל הוא נקרא אינטגרל רימן, והתפקוד המתקבל מלווה בקבוע שרירותי. אינטגרל בלתי מוגדר יוצר לעתים קרובות משפחה של פונקציות; לכן, האינטגרל הוא בלתי מוגדר. אינטגרלים ותהליך האינטגרציה נמצאים בלב פתרון משוואות דיפרנציאליות. עם זאת, שלא כמו השלבים בידול, צעדים אינטגרציה לא תמיד בצע שגרתית ברורה. מדי פעם, אנו רואים כי הפתרון אינו יכול לבוא לידי ביטוי במפורש במונחים של פונקציה בסיסית. במקרה זה, הפתרון האנליטי ניתן לעתים קרובות בצורה של אינטגרל בלתי מוגדר.

תורת החישוב הבסיסית

המובהק והאינטגרל הבלתי מוגדר מקושרים לפי תורת החישוב הבסיסית כדלקמן: כדי לחשב

אינטגרל מובהק , מצא את אינטגרל בלתי מוגדר > (ידוע גם בשם האנטי נגזרת) של הפונקציה ולהעריך בנקודות הקצה x = a ו- x = b . ההבדל בין אינטגרלים מוגדרים בלתי מוגדרים יהיה ברור כאשר אנו מעריכים את האינטגרלים עבור אותה פונקציה. שקול את האינטגרל הבא: אישור. בואו נעשה את שניהם ונראה את ההבדל.

עבור אינטגרציה, אנחנו צריכים להוסיף אחד למדד אשר מוביל אותנו אל הביטוי הבא:

בשלב זה של זמן

C

הוא רק קבוע לנו. נדרש מידע נוסף לבעיה כדי לקבוע את הערך המדויק של

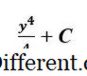
C . תן לנו להעריך את אותו אינטגרל בצורתו המוגדרת i. ה., כאשר הגבול העליון והתחתון כלל. מבחינה גרפית, אנו מחשבים כעת את השטח מתחת לעיקול f (x) = y

3

בין y = 2 ^ו- y = 3 > הצעד הראשון בהערכה זו הוא זהה להערכה אינטגרלית בלתי מוגבלת. ההבדל היחיד הוא שהפעם אנחנו לא מוסיפים את הקבוע C . הביטוי במקרה זה נראה כדלקמן:

זה מוביל מוביל: בעיקרו של דבר, התחלנו 3 ולאחר מכן 2 בביטוי וקיבל את ההבדל ביניהם. זהו הערך המובהק לעומת השימוש בקבוע

C

קודם לכן.

בואו לחקור את גורם קבוע (לגבי אינטגרל בלתי מוגדר) בפירוט קצת יותר.

אם ההפרש של y 3

הוא

3y 2 ^{, ולאחר מכן} ∫ 3y ² dy = y

3 עם זאת, ^3y 2 ^{יכול להיות הפרש של ביטויים רבים שחלקם כוללים}

y 3 ^-5 , > y 3 ⁺⁷ , וכו '… משמעות הדבר היא שההיפוך אינו ייחודי מאחר שהמתמיד אינו ידוע במהלך הפעולה. אז באופן כללי, 3y ² הוא ההפרש של y

3 + C ^כאשר C הוא קבוע. אגב, C ידוע בתור ^{קבוע של אינטגרציה '}. אנחנו כותבים את זה בתור: ∫ 3y 2. dx = y

3

+ C טכניקות אינטגרציה של אינטגרל בלתי מוגדר, כגון בדיקת טבלה או אינטגרציה של Risch, יכולות להוסיף אי-רציפויות חדשות בתהליך האינטגרציה. אלה הפסקות חדשות מופיעות כי אנטי נגזרות יכול לדרוש את הכניסה של לוגריתמים מורכבים. ^{לוגריתמים מורכבים יש חוסר רציפות קפיצה כאשר הטענה חוצה את הציר השלילי האמיתי, ואלגוריתמים אינטגרציה לפעמים לא יכול למצוא ייצוג שבו קפיצות אלה לבטל.} אם נבחן את האינטגרל המובהק באמצעות חישוב ראשון של אינטגרל בלתי מוגדר ולאחר מכן החלפת גבולות האינטגרציה בתוצאה, עלינו להיות מודעים לכך שאינטגרציה בלתי מוגבלת עלולה ליצור אי-רציפות. אם כן, עלינו לחקור את הפסקות באינטגרציה של האינטגרציה.