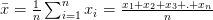ההבדל בין חציון וממוצע (ממוצע): חציון לעומת ממוצע (ממוצע)
חציון לעומת ממוצע (ממוצע)
חציון וממוצע הם אמצעים של נטייה מרכזית בסטטיסטיקה תיאורית. לעתים קרובות ממוצע אריתמטי נחשב כממוצע של תצפיות. לכן, כאן הוא נחשב כממוצע. עם זאת, הממוצע אינו הממוצע האריתמטי בכל הזמנים.
ממוצע
הממוצע האריתמטי הוא סכום ערכי הנתונים חלקי מספר ערכי הנתונים, i. ה.
- <->אם הנתונים ממרחב מדגם זה נקרא מדגם ממוצע (

לדוגמה, לשקול את ההכנסה הממוצעת של אזרחי עיר מסוימת. מאחר שכל ערכי הנתונים מסוכמים ומתחלקים, ההכנסה של אדם עשיר מאוד משפיעה על הממוצע באופן משמעותי. לכן, הערכים הממוצעים אינם מייצגים טוב את הנתונים תמיד.
כמו כן, במקרה של אות לסירוגין, הנוכחי עובר דרך אלמנט מעת לעת משתנה מהכיוון החיובי לכיוון השלילי ולהיפך. אם ניקח את הזרם הממוצע העובר דרך האלמנט בתקופה אחת, הוא ייתן 0, כלומר, שום זרם לא עבר את האלמנט, וזה כמובן לא נכון. לכן, גם במקרה זה, ממוצע אריתמטי אינו מדד טוב.
הממוצע האריתמטי הוא אינדיקטור טוב כאשר הנתונים מופצים באופן שווה. עבור התפלגות נורמלית, הממוצע שווה למצב ולחציון. כמו כן, יש את שאריות הנמוך ביותר כאשר בוחנים את השורש הממוצע שגיאה בריבוע; לכן, המדד הטוב ביותר כאשר הוא נדרש לייצג נתונים על ידי מספר אחד.
חציון
הערכים של נקודת הנתונים האמצעית לאחר סידור כל ערכי הנתונים בסדר עולה מוגדר כחציון של מערך הנתונים.
אם מספר התצפיות (נקודות נתונים) הוא מוזר, אז החציון הוא התצפית בדיוק באמצע הרשימה המסודרת.
• אם מספר התצפיות (נקודות נתונים) הוא אפילו, אז החציון הוא הממוצע של שתי תצפיות באמצע ברשימה הורה.
מדיאן מחלק את התצפית לשתי קבוצות; אני. ה. קבוצה (50%) של ערכים גבוהים יותר וקבוצה (50%) של ערכים נמוכים מהחציון. מדיומים משמשים באופן ספציפי בהפצות מוטות ומייצגים נתונים טובים יותר מהממוצע האריתמטי.
חציון לעומת ממוצע (ממוצע)
• הממוצע והחציון הם מדדים של נטייה מרכזית ומסכמים את הנתונים. ממוצע הוא עצמאי של המיקום של נקודות נתונים, אבל החציון מחושב באמצעות המיקום.
• ממוצע מושפע מאוד על ידי חריגים בעוד החציון אינו מושפע.
לכן, החציון הוא מדד טוב יותר מהממוצע במקרים של התפלגויות מאוד מוטות.
• בהתפלגות הרגילה, הנורמלית, האמצעים והחציון זהים.