ההבדל בין פרבולה להיפרבולה
פרבולה לעומת היפרבוליה
קפלר תיאר את מסלולי כוכבי הלכת כמו אליפסות אשר שונה מאוחר יותר על ידי ניוטון כפי שהוא הראה מסלולים אלה כדי להיות חלקים מיוחדים חרוט כגון פרבולה היפרבולה. יש קווי דמיון רבים בין פרבולה לבין היפרבולה אבל יש הבדלים גם יש משוואות שונות כדי לפתור בעיות גיאומטריות מעורבים אלה חרוטי קטעים. כדי להבין טוב יותר את ההבדלים בין פרבולה לבין היפרבולה, אנחנו צריכים להבין את החלקים האלה חרוט.
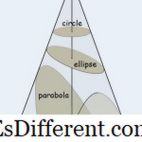
Image באדיבות: // cseligman. com
קטע הוא משטח או מתאר של משטח זה נוצר על ידי חיתוך דמות מוצקה עם מטוס. אם הדמות מוצק קורה להיות קונוס, עקומת שהתקבל נקרא קטע חרוט. סוג וצורה של החלק חרוט נקבע על ידי זווית הצומת של המטוס ואת ציר החרוט. כאשר החרוט נחתך בזווית ישרה אל הציר, אנו מקבלים צורה עגולה. כאשר לחתוך פחות זווית ישרה, אבל יותר זווית שנעשו על ידי הצד של קונוס התוצאות של אליפסה. כאשר לחתוך מקביל בצד החרוט, עקומת המתקבל הוא פרבולה וכאשר לחתוך כמעט במקביל לציר כי לצד, אנחנו מקבלים עקומה המכונה היפרבולה. כפי שניתן לראות מן הדמויות, עיגולים אליפסות הם עקומות סגורות בעוד פרבולות hyperbolas הם עקומות פתוחות. במקרה של פרבולה, שתי הזרועות הופכות בסופו של דבר מקבילות זו לזו, ואילו במקרה של היפרבולה זה לא כך.
-> ->מאז מעגלים ו parabolas נוצרים על ידי חיתוך קונוס בזוויות ספציפיות, כל המעגלים זהים בצורת כל פרבולות זהים בצורתם. במקרה של hyperbolas ו אליפסות יש מגוון רחב של זוויות בין המטוס לבין הציר ולכן הם נוטים להיות מגוון רחב של צורות. המשוואות של ארבעת הסעיפים של חרוט הם כדלקמן.
מעגל x 2 + y 2 = 1
אליפסה- x 2 / a 2 + y 2 / b 2 1 > <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
= 1




