ההבדל בין שגיאה מוחלטת לבין שגיאה יחסית | שגיאה מוחלטת לעומת שגיאה יחסית
הפרש קיומו - שגיאה מוחלטת לעומת שגיאה יחסית
שגיאה מוחלטת ושגיאה יחסית הן שתי דרכים להצביע טעויות במדידות הניסוי למרות שקיים הבדל בין שגיאה מוחלטת לשגיאה יחסית על סמך החישוב שלהם. רוב המדידות בניסויים מדעיים מורכבים מטעויות, עקב טעויות אינסטרומנטליות וטעויות אנוש. בחלק מהמקרים, עבור מכשיר מדידה מסוים, קיים ערך קבוע קבוע מראש עבור שגיאה מוחלטת (הקריאה הקטנה ביותר, לדוגמה: - סרגל = +/- 1 מ"מ) זה ההבדל בין true ערך וערך הניסוי. עם זאת, השגיאה היחסית משתנה בהתאם לערך הניסוי ואת השגיאה המוחלטת. זה נקבע על ידי לקיחת היחס של טעות מוחלטת ואת הערך הניסויי. לכן, ההבדל בין ההבדל בין השגיאה המוחלטת לשגיאה היחסית הוא שגיאה מוחלטת הוא גודל ההבדל בין הערך המדויק לבין קירוב בעוד השגיאה היחסית מחושבת על ידי חלוקת השגיאה המוחלטת לפי גודל הערך המדויק. -> ->
מהי שגיאה מוחלטת?שגיאה מוחלטת היא אינדיקציה לאי הוודאות של המדידה. במילים אחרות, הוא מודד באיזו מידה, הערך האמיתי יכול להשתנות מערכו הניסויי. שגיאה מוחלטת מתבטאת באותן יחידות כמו המדידה.
דוגמה:
נניח שאנחנו רוצים למדוד את אורך העיפרון באמצעות סרגל עם סימן מילימטר. אנו יכולים למדוד את אורכו לערך המילימטר הקרוב ביותר. אם אתה מקבל את הערך כמו 125 מ"מ, זה מתבטא 125 + / - 1 מ"מ. השגיאה המוחלטת היא +/- 1 מ"מ. -> ->
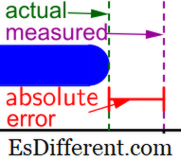
טעות יחסית תלויה בשני משתנים; טעות מוחלטת וערך ניסיוני של המדידה. לכן, שני פרמטרים אלה צריכים להיות ידועים, כדי לחשב את השגיאה היחסית. השגיאה היחסית מחושבת על ידי היחס בין השגיאה המוחלטת לבין הערך הניסויי. הוא מתבטא באחוזים או בשבריר; כך שאין לו יחידות.
->
טעות יחסית של אינטגרציה מונטה קרלו לחשב pi
מה ההבדל בין שגיאה מוחלטת שגיאה יחסית?
שגיאה מוחלטת היא ערך Δx (+ או - value), כאשר x הוא משתנה; זוהי טעות פיזית במדידה.זה ידוע גם את השגיאה בפועל במדידה.
במילים אחרות, זה ההבדל בין הערך האמיתי לבין הערך הניסיוני.
- diff מאמר ממוצע לפני טבלה ->
שגיאה מוחלטת = ערך ממשי - ערך מדידה
טעות יחסית:
טעות יחסית היא היחס בין השגיאה המוחלטת (Δx) לבין הערך הנמדד (x). זה בא לידי ביטוי כאחוז (אחוז טעות) או כשבריר (אי וודאות חלקי).
יחידות וחישוב של שגיאה מוחלטת וטעות יחסית |
יחידות
שגיאה מוחלטת:

יש לה אותן יחידות כמו הערך הנמדד. לדוגמה, אם מודדים את אורך הספר בסנטימטרים (ס"מ), השגיאה המוחלטת כוללת גם את אותן יחידות.
שגיאת יחסית:
שגיאה יחסית יכולה להתבטא כשבר או כאחוז. עם זאת, לשניהם אין יחידה בערך.
חישוב שגיאה
דוגמה 1:
אורך הקרקע בפועל הוא 500 רגל. מכשיר מדידה מציג את אורך כדי להיות 508 מטר.
שגיאה מוחלטת:
| שגיאה מוחלטת = [ערך ממשי - ערך נמדד] = [508-500] רגל = 8 רגל טעות יחסית: |
כאחוז:
כקטע: דוגמה 2:
סטודנט רצה למדוד את גובה הקיר בחדר. הוא מדד את הערך באמצעות סרגל מטר (עם ערכי מילימטר), זה היה 3. 215m.
שגיאה מוחלטת:

שגיאה מוחלטת = +/- 1 מ"מ = +/- 0. 001m

(קריאה קטנה ביותר שניתן לקרוא באמצעות השליט)
| שגיאה יחסית: |
שגיאת יחסית = שגיאה מוחלטת = ערך ניסיוני = 0. 001 m ÷ 3. 215 m * 100 = 0. 0003%
תמונה באדיבות: "שגיאה מוחלטת" של DEMcAdams - עבודה עצמאית. (CC BY-SA 4. 0) באמצעות ויקישיתוף "טעות יחסית של אינטגרציה מונטה קרלו לחשב pi" על ידי Jorgecarleitao - python ו xmgrace. (CC BY-SA 3. 0) באמצעות ויקיפדיה




