ההבדל בין הבחנה לבין נגזרות

דיפרנציאציה לעומת נגזרת

בחישוב דיפרנציאלי, נגזרת והבחנה קשורים זה לזה, אך שונים מאוד, ומשמשים לייצוג שני מתמטיים חשובים מושגים הקשורים לפונקציות.

מהו נגזר?

נגזרת של פונקציה מודדת את השיעור שבו ערך הפונקציה משתנה עם כניסת הקלט. בפונקציות מרובות המשתנים, השינוי בערך הפונקציה תלוי בכיוון השינוי בערכים של המשתנים הבלתי תלויים. לכן, במקרים כאלה, נבחר כיוון מסוים והפונקציה מובחנת בכיוון מסוים זה. נגזר זה נקרא נגזרת כיוונית. נגזרים חלקיים הם סוג מיוחד של נגזרים כיווניים.

-> ->

נגזרת של פונקציה בעלת ערך וקטורי f יכולה להיות מוגדרת כמגבלה

בכל מקום שהיא קיימת. כפי שצוין קודם, זה נותן לנו את קצב הגידול של הפונקציה f בכיוון הווקטור u. במקרה של פונקציה בעלת ערך יחיד, זה מפחית את ההגדרה הידועה של נגזרת,

לדוגמה,

משתנה בכל מקום, והנגזרת שווה לגבול,

, שהוא שווה ל-

. הנגזרות של פונקציות כגון

קיימות בכל מקום. הם בהתאמה שווה את הפונקציות

.

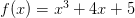
זה ידוע בשם נגזרת הראשונה. בדרך כלל הנגזרת הראשונה של הפונקציה f מסומנת על ידי f ⁽¹⁾ . עכשיו באמצעות סימון זה, ניתן להגדיר נגזרים סדר גבוה יותר.

הוא נגזרת הכיוון השנייה, ומציינת את n נגזרת על ידי f ⁽ⁿ⁾ עבור כל n,

, מגדיר את n נגזרת.

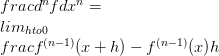
מה ההבדל?

דיפרנציאציה היא תהליך של מציאת הנגזרת של פונקציה אחרת. D- אופרטור מסומן על ידי D מייצג בידול בכמה הקשרים. אם x הוא המשתנה הבלתי תלוי, ולאחר מכן D ≡ ^d / _dx . D- מפעיל הוא מפעיל ליניארי, אני. ה. עבור כל שתי פונקציות שונות f ו g וקבוע c, תכונות הבאות מחזיקות.

אני. D (f g) = D (f) + D (g)

II. D cd (f

. D f g> = D (f) g + f (<)> <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< G f> <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< o ^g ) = ( _D ( ^{f) o g) D (g). לדוגמה, כאשר F (x) =} x ₂ ^חטא x מובחן ביחס ל x הכללים שניתנו, התשובה תהיה 2 x חטא x - + x 2 cos x. מה ההבדל בין בידול לבין נגזרת? • נגזרת מתייחסת לשיעור שינוי של פונקציה

• דיפרנציאציה היא תהליך מציאת הנגזרת של פונקציה.