הפרש בין נגזרות ודיפרנציאליות

נגזרים לעומת דיפרנציאלים

בחישוב דיפרנציאלי, נגזרות ודיפרנציאליות של פונקציה קשורות קשר הדוק אך יש להן משמעויות שונות מאוד, שימשו לייצוג שני אובייקטים מתמטיים חשובים הקשורים לפונקציות שונות.

מהו נגזר?

נגזרת של פונקציה מודדת את השיעור שבו ערך הפונקציה משתנה עם כניסת הקלט. בפונקציות מרובות המשתנים, השינוי בערך הפונקציה תלוי בכיוון השינוי בערכים של המשתנים הבלתי תלויים. לכן, במקרים כאלה, נבחר כיוון מסוים והפונקציה מובחנת בכיוון מסוים זה. נגזר זה נקרא נגזרת כיוונית. נגזרים חלקיים הם סוג מיוחד של נגזרים כיווניים.

-> ->

נגזרת של פונקציה בעלת ערך וקטורי f יכולה להיות מוגדרת כמגבלה

בכל מקום שהיא קיימת. כפי שצוין קודם, זה נותן לנו את קצב הגידול של הפונקציה f בכיוון הווקטור u. במקרה של פונקציה בעלת ערך יחיד, זה מפחית את ההגדרה הידועה של נגזרת,

לדוגמה,

משתנה בכל מקום, והנגזרת שווה לגבול,

, שהוא שווה ל-

. הנגזרות של פונקציות כגון

קיימות בכל מקום. הם בהתאמה שווה את הפונקציות

.

זה ידוע בשם נגזרת הראשונה. בדרך כלל הנגזרת הראשונה של הפונקציה f מסומנת על ידי f ⁽¹⁾ . עכשיו באמצעות סימון זה, ניתן להגדיר נגזרים סדר גבוה יותר.

הוא נגזרת הכיוון השנייה, ומציינת את n נגזרת על ידי f ⁽ⁿ⁾ עבור כל n,

, מגדיר את n נגזרת.

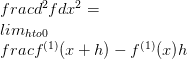
מה ההבדל?

דיפרנציאל של פונקציה מייצג את השינוי בפונקציה ביחס לשינויים במשתנה או המשתנים הבלתי תלויים. בסימון הרגיל, עבור פונקציה מסוימת f של משתנה יחיד x, ההפרש הכולל של ההזמנה 1 df הוא שניתן על ידי

. משמעות הדבר היא ששינוי זעיר ב x ((1) (x <) d x שנה ב f. שימוש במגבלות אחד יכול בסופו של דבר עם הגדרה זו כדלקמן. נניח ש Δ

x הוא השינוי ב x בנקודה שרירותית x ו- Δ f הוא השינוי המקביל בפונקציה. ניתן להראות כי Δ f = f (1) ⁽ x) Δ x + ε, היכן ε הטעות. עכשיו, הגבול Δ x → 0 Δ ^f Δ _{x =} f (1) <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< > 0 =.לכן ניתן להסיק כי Δ ^{x →} 0 ε = 0. כעת, מציין את Δ x → 0 Δ ^f כמו d _{f ו Δ} x → 0 Δ x כמו x ההגדרה של ההפרש מתקבלת בקפדנות. לדוגמה, ההפרש של הפונקציה הוא. במקרה של פונקציות של שני משתנים או יותר, ההפרש הכולל של פונקציה מוגדר כסכום של הפרשים בכיוונים של כל המשתנים הבלתי תלויים. מבחינה מתמטית, ניתן לומר זאת כ-. מה ההבדל בין נגזר לבין דיפרנציאלי? • נגזרים מתייחסים לשיעור שינוי של פונקציה ואילו ההפרש מתייחס לשינוי בפועל של הפונקציה, כאשר המשתנה הבלתי תלוי נתון לשינוי. • הנגזרת ניתנת על ידי, אך ההפרש ניתן על ידי.