ההבדל בין מספרים רציונליים ומספרים לא רציונליים ההבדל בין

המונח "מספרים" מזכיר לנו מה מסווגים בדרך כלל כערכים שלמים וחיוביים גדולים מאפס. סוגים אחרים של מספרים כוללים מספרים שלמים ו- שברים , מורכבים ו- מספרים ממשיים וגם ערכים שליליים שלמים .

מרחיבים את הסיווגים של מספרים נוספים, אנו נתקלים ב רציונליים ו- מספרים לא רציונליים . מספר רציונלי הוא מספר שניתן לכתוב כשבריר. במילים אחרות, המספר הרציונלי יכול להיכתב כשיעור של שני מספרים.

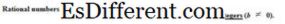
שקול, לדוגמה, את המספר 6 . זה יכול להיות כתוב כמו היחס של שני מספרים דהינו. 6 ו- 1 , מה שמוביל ליחס 6/1 . כמו כן, 2/3 , אשר נכתב כמו שבר, הוא מספר רציונלי.

אנו יכולים, אם כן, להגדיר מספר רציונלי, כמספר שנכתב בצורת שבר, שבו הן המונה (המספר למעלה) והמכנה (המספר בתחתית) הם מספרים שלמים. מעצם הגדרתו, כל מספר שלם הוא גם מספר רציונלי.

->

יחס של שני מספרים גדולים כגון ( 129, 367, 871 ) / ( 547, 724, 863 ) יהווה גם דוגמה למספר רציונלי מהסיבה הפשוטה שגם המונה וגם המכנה הם מספרים שלמים. לעומת זאת, כל מספר שלא ניתן לבטא בצורה של שבר או יחס מוגדר כבלתי רציונלי. הדוגמה הנפוצה ביותר של מספר לא רציונלי היא

√ 2 ( 1. 414213 … . דוגמה פופולארית נוספת למספר לא רציונלי היא המספר המספרי π ( 3. 141592 … ) .

מספר לא הגיוני יכול להיות כתוב כעשרונית, אבל לא כמו חלק. מספרים לא רציונליים אינם משמשים לעתים קרובות בחיי היומיום למרות שהם קיימים על הקו מספר. יש מספר אינסופי של מספרים לא הגיוניים בין

0 ו- 1 על מספר השורה. למספר לא רציונלי יש ספרות אינסופיות וחוזרות על ימין של הנקודה העשרונית. -> ->

שים לב שהערך המצוין של

22/7 עבור הקבוע π הוא למעשה רק אחד מהערכים של π > בהגדרה, היקף המעגל מחולק פעמיים ברדיוס שלו הוא הערך של π. זה מוביל למספר ערכים של π , כולל, אך לא רק, 333/106, 355/113 וכן הלאה. רק השורשים הריבועיים של המספרים הריבועים; אני. ה., השורשים הריבועיים של הריבועים המושלמים

הם רציונליים. - <->

(1 רציף) (> לא רציונלי)

√3 (לא רציונלי)

√4 < = 2 (> רציונלי)

√5, √6, √7, √8 (לא רציונלי) √9

= 3 (רציונלי) וכן הלאה.

יתר על כן, נציין כי רק n השורשים של

n הכוחות הרציונליים הם רציונליים. לכן, 6 שורש 64 הוא הגיוני, משום ש- 64 הוא 6 כוח, כלומר 6 כוח של 2 . אבל 6 השורש של 63 הוא לא הגיוני. 63 אינו מושלם 6 כוח.

באופן בלתי נמנע, ייצוג עשרוני של אי רציונלי נכנס לתמונה ומציג כמה תוצאות מעניינות. כאשר אנו מבטאים מספר

רציונאלי

כעשרונית, אזי העשרונית תהיה

מדויקת (כמו 1/5 = 0. 20) או שזה יהיה לא מדויק (כמו, 1/3 ≈ 0. 3333 ). בכל מקרה, יהיה דפוס צפוי של ספרות. שים לב שכאשר המספר לא רציונאלי מבוטא כעשרונית, אז ברור שזה לא יהיה מדויק, כי אחרת, המספר יהיה הגיוני. יתר על כן, לא יהיה דפוס צפוי של ספרות. לדוגמה, √2 ≈ 1. 4142135623730950488016887242097

כעת, עם מספרים רציונליים, אנו נתקלים מדי פעם

1/11 = 0. 0909090 .

השימוש בשני הסימנים השווים ( =) ושלוש נקודות ( אליפסה) מרמז על כך שאף על פי שלא ניתן לבטא את 1/11 בדיוק כמו עשרוני, אנחנו עדיין יכולים לשער אותו עם ספרות עשרוניות רבות כמו מותר להגיע קרוב ל 1/11 . לכן, הצורה העשרונית של 1/11 נחשבת לא מדויקת. באותה מידה, הצורה העשרונית של ¼

שהיא 0. 25, היא מדויקת. בהגיעם לטופס העשרוני למספרים לא רציונליים, הם יהיו תמיד לא מדויקים. אם נמשיך עם הדוגמה של √ 2 , כאשר אנו כותבים

√2 = 1. 41421356237 … (שימו לב לשימוש באליפסות), זה מיד מרמז כי לא עשרוני עבור > √2 יהיה מדויק. יתר על כן, לא יהיה דפוס צפוי של ספרות. בעזרת מושגים משיטות נומריות, שוב, אנו יכולים להתקרב באופן רציונלי למספר ספרות עשרוני עד לנקודה כזו שאנו קרובים ל √2 . כל הערה על מספרים רציונאליים ואי-רציונליים אינה יכולה להסתיים ללא הוכחה הכרחית מדוע √2 הוא לא רציונלי. בעשותנו כך, אנחנו גם להבהיר, את הדוגמה הקלאסית של הוכחה על ידי המשך רדיוגרפיה. נניח √2 הוא רציונלי. זה מוביל אותנו לייצג אותו כיחס של שני מספרים שלמים, אומרים

p ו q

.

√2 = p / q למותר לציין, p ו- q

אין גורמים נפוצים, שכן אם היו גורמים משותפים, היינו מבטלים אותם מתוך המונה והמכנה.

ריבוע שני צידי המשוואה, אנו בסופו של דבר, -> 2

2 / q 2

זה יכול להיות כתוב בנוחות כמו,

p

2 = 2q > 2 המשוואה האחרונה מראה כי p

2

הוא אפילו. זה אפשרי רק אם p עצמו הוא אפילו. זה בתורו מרמז כי p

2 הוא מתחלק על ידי 4 . לפיכך, q 2 וכתוצאה מכך q חייב להיות אפילו.אז p ו- q הן אף סותרות את ההנחה הראשונית שלנו שאין להן גורמים משותפים. לכן, √2 לא יכול להיות הגיוני. ש 'ד' -> -